承接上文一段胡编乱造假模假样的山寨绘制方法后,本篇正式开始做科学的研究。
上篇地址:
齿轮(gear)和齿条(rack)有相当一部分的概念是重合的,但是这些概念绝大部分先从齿轮诞生,也即是这些参数的换算关系中,免不了和圆周率pi有一定关联。
考虑到这篇文章是以非机械专业的角度入手,我们还是先从简单的齿条开始。一旦涉及到圆周率pi的出现,在文中会有特殊的提示。
在介绍齿条之前,我们先介绍齿轮/齿条的三大基本概念或基本参数:
齿数,模数压力角随后我们在介绍齿条的过程中,仅展开介绍和齿条相关的两组重要参数:
齿根高和齿顶高齿距和齿厚基本概念1:齿数(Number of teeth, N)
首先我们介绍最容易理解的齿数:一个齿轮中齿的数量。
在这里需要明确的是,为了方便理解和严谨推论,对齿条来说,我们认为“齿数”是没有意义的,齿数仅对齿轮来说有意义。因为齿数的改变会对齿轮的造型形成重大影响,而齿条的齿数仅仅是简单的重复叠加。

如上图,左侧的齿轮有10个齿,齿数=10,右侧齿数=15。
观察可以发现,该图中两个齿轮单个齿的大小基本相同,实际上由程序生成的这两个齿轮是可以配合工作的(关于齿轮匹配的问题,会在下篇详细讲解)。在这种情况下,齿数直接决定了整个齿轮的大小。齿数多的齿轮自然就更大。
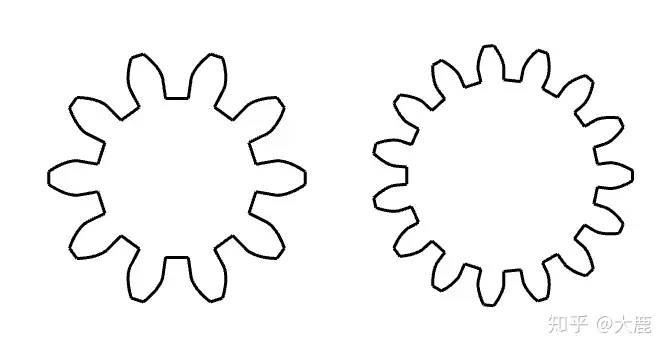
而在上图中,齿数仍然是10和15,但是右侧的齿轮单个齿变小了,使得他最后整体尺寸和左侧差不多。
显而易见,这两个齿轮的单个齿大小不同,他们无法配合在一起工作。
理解了齿的数量以后,我们自然就想到如何评估单个齿的大小,在这里我们引入第二个重要概念:模数
基本概念2:模数(Module, m)
重点1:决定齿的大小,而不是齿轮的大小
在这里要特别注意的是,模数决定的是单个齿的大小,而不是整个齿轮的大小。
根据上文我们对齿数的了解,齿轮的整体大小由“齿的数量”和“单个齿的大小”这两个因子共同决定。
重点2:模数是齿轮的最基本参数
齿轮的几个其他重要参数:齿距(pitch),齿厚(thickness),齿顶高(addendum),齿根高(dedendum),分度圆直径(pitch diameter)等等,均由模数计算得到。确定齿轮的各项参数之前,必须先确定模数。
绿色:虽然随着技术的进步,齿轮的模数没有从前那么重要,但是作为科普基础理论的文章,我们在这里还是采用最基本最简单的模数,而不讨论任何非标的情况。

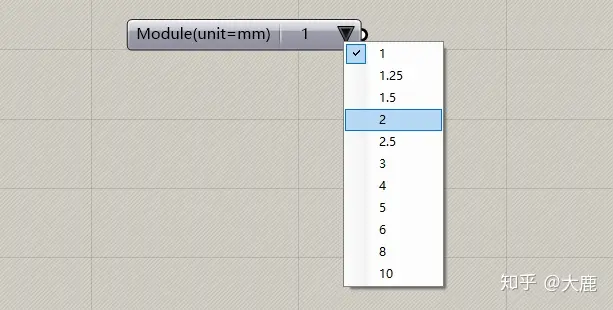
如图,我们在文章中将会使用我国标准模数系列表第一系列的1-10制作成Grasshopper的value list电池,不采用第二系列和括号内的模数。单位选取毫米。
基本概念3:压力角(Pressure angle, θ\theta )
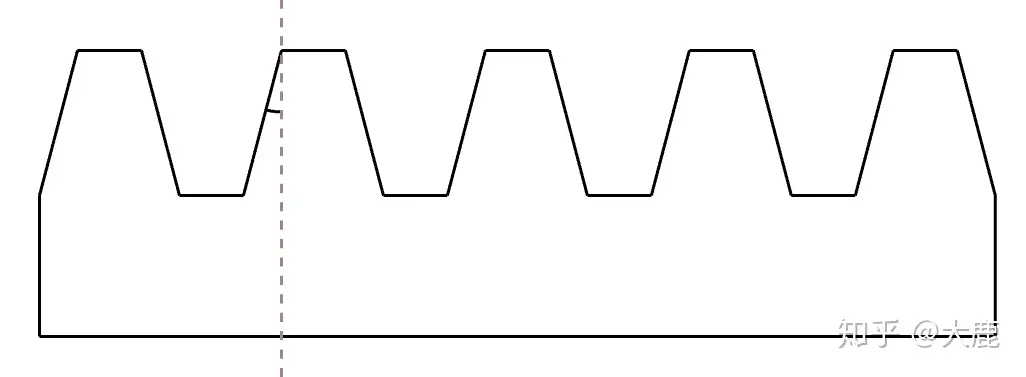
齿轮的压力角刚开始理解起来会比较复杂。因为齿轮的侧面均为曲线,但对齿条来说这个概念非常简单,如上图,压力角就是齿的侧面斜线和垂直虚线之间的夹角。称之为 θ\theta 。
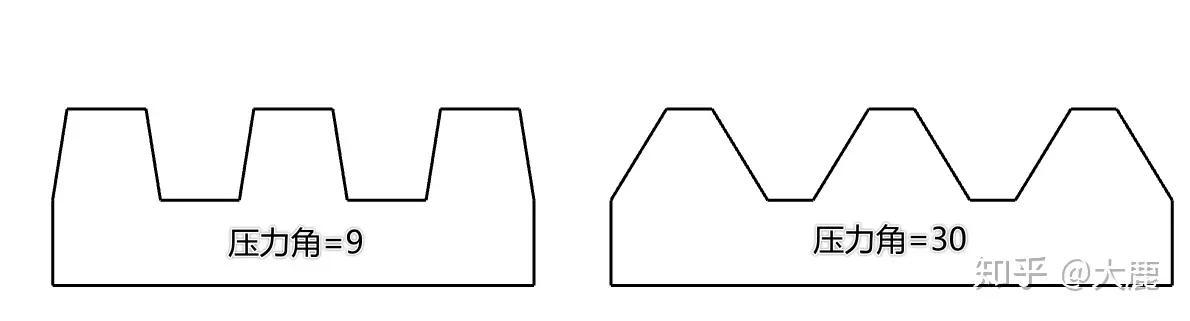
压力角越小,齿的侧面越陡峭,反之压力角越大,齿的侧面越平缓。
上图的两个齿条看起来都不太好用的样子,是因为压力角太大或者太小。我国规定齿轮的标准压力角为20度。
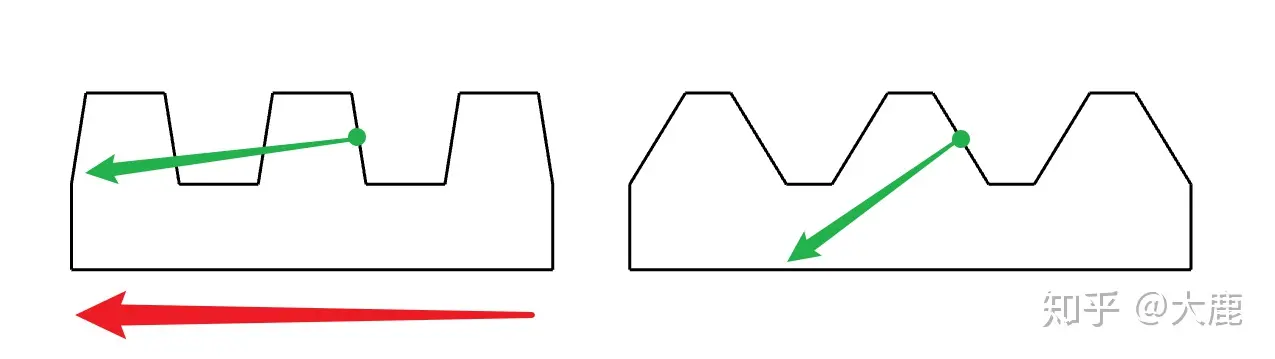
压力角影响的是齿条在传动过程中的受力方向。在上图中,假设齿条的运动为水平从右往左,如上图红色箭头。而两个齿条收到的压力直接作用在齿侧面的这条斜线上,压力呈绿色箭头方向。
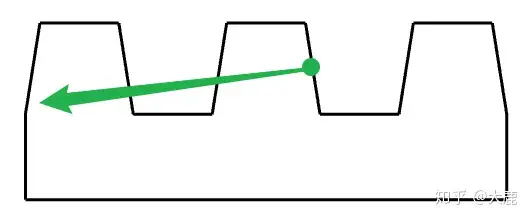
左侧齿条受到的力和水平方向夹角很小,显而易见只有很少部分的力垂直往下作用于齿条,该齿条的传动效率较高。
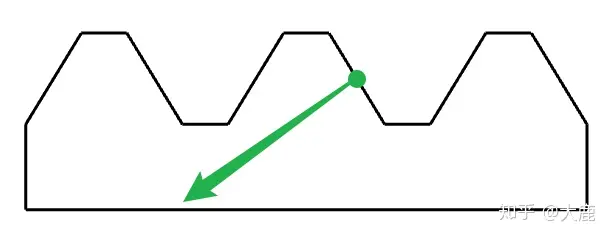
而压力角比较大的情况,如上图右侧,会发现齿条受到的力和水平方向夹角很大,有比较大一部分的分力垂直往下作用于齿条。这部分力对齿条来说就是垂直于运动方向的力,对齿轮来说就是对准旋转中心的力。这部分力全部浪费并没有作用在传动过程中,因此右侧的齿条效率很低。
既然如此,为什么我们不直接让压力角尽量减少呢?
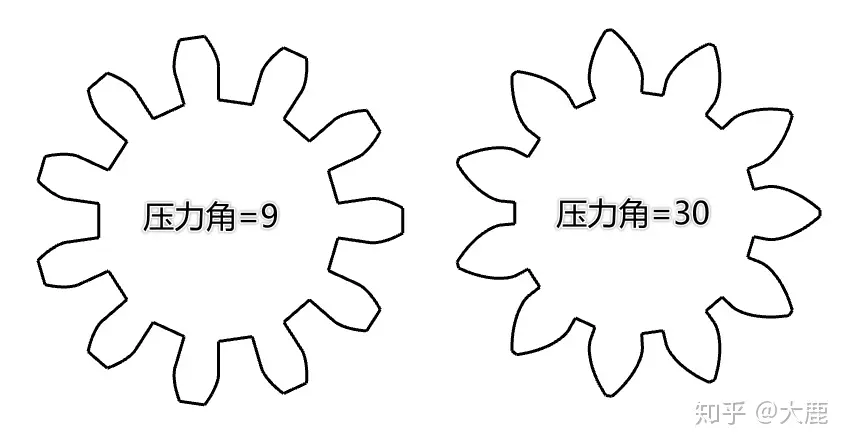

我们尝试把压力角落实到齿轮上查看效果,并回顾刚才的两种齿条。
压力角小的齿轮虽然效率高,但我们也会很容易发现一些问题:愣头青一般不友好的状态,很难和别的齿轮齿条合作,而齿根位置太薄,也容易受到冲击力而断裂。因此压力角太小也不是什么好事,本文和下篇中我们选取最常见的压力角=20度,在Grasshopper中为了方便研究压力角改变带来的效果,我们选用0-30度的滑动条。

概念4:分度线(Pitch line),齿顶高(addendum)和齿根高(dedendum)
首先忽略后面两个完全搞不清怎么念的单词。
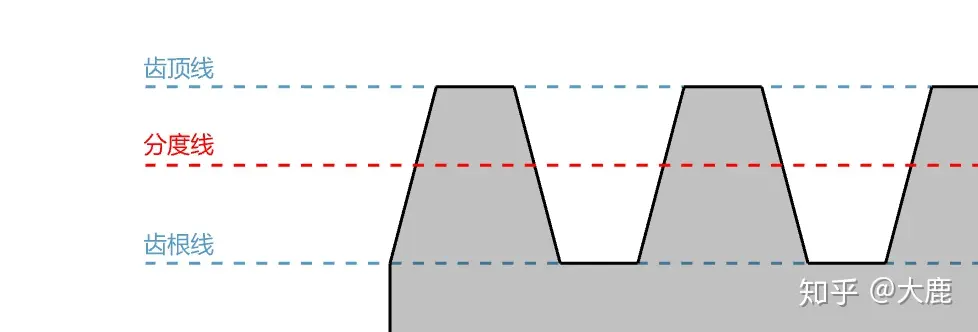
我们先介绍齿条水平方向的三条基准线。这三条线决定了齿条垂直方向的尺寸。
分别是红色的分度线,蓝色的齿顶线(addendum line)和齿根线(dedendum line)。后两者顾名思义,为齿条顶部和根部的基准线。
中间的分度线比较特殊,这条线是齿轮和齿条中最关键的定位线。在齿轮中被称为分度圆(Pitch circle),该圆的半径和模数有直接关系。这一点来说和齿条不同。因为在齿条中分度线是一个直线,而不是一个有固定大小的圆。
在定位或绘制齿条时,分度线是首先考量的元素。
再仔细观察这条线的位置时,我们发现他并不是齿顶线和齿根线的居中线。看起来这条线离开齿顶更近一些。
此时我们再引入齿顶高和齿根高这两个概念。
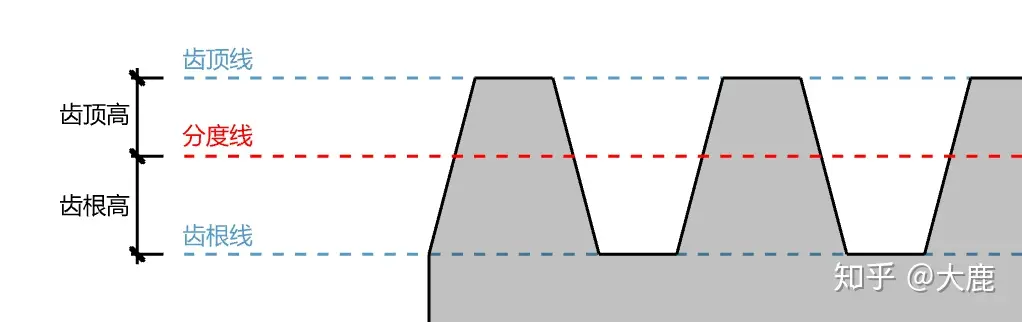
如上图,齿顶线和分度线的距离为齿顶高,同理,齿根线和分度线的距离为齿根高。
在绘制齿轮时,正确的顺序是优先确定分度线,随后确定齿顶高和齿根高,最后由前三个参数确定齿顶线和齿根线。
至于为什么分度线不是想象中的齿顶和齿根的中间线。我们再查看一下标准齿轮种对齿顶和齿根高的定义:
齿顶高=模数 x 齿顶高系数
齿根高=齿顶高 x(1 + 顶隙系数)
通常情况下,标准齿轮的齿顶高系数=1,顶隙系数=0.25。
也就是说公式可以简化为:
齿顶高=模数
齿根高=1.25 x 模数
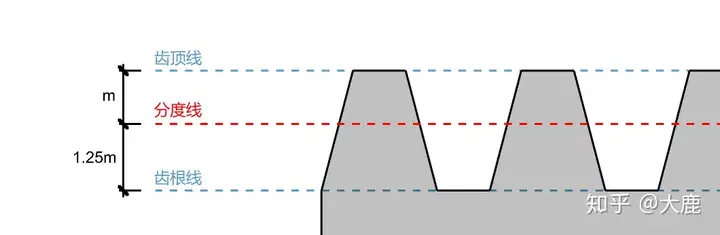
如上图。模数=m。分度线向上平移m为齿顶线,向下平移1.25m为齿根线。齿的总深度=2.25 x 模数。分度线在整个齿纵向的4:5位置。
至此,齿条的垂直向参数就介绍完毕了。
概念5:齿距(Pitch, P)和齿厚(Thickness)
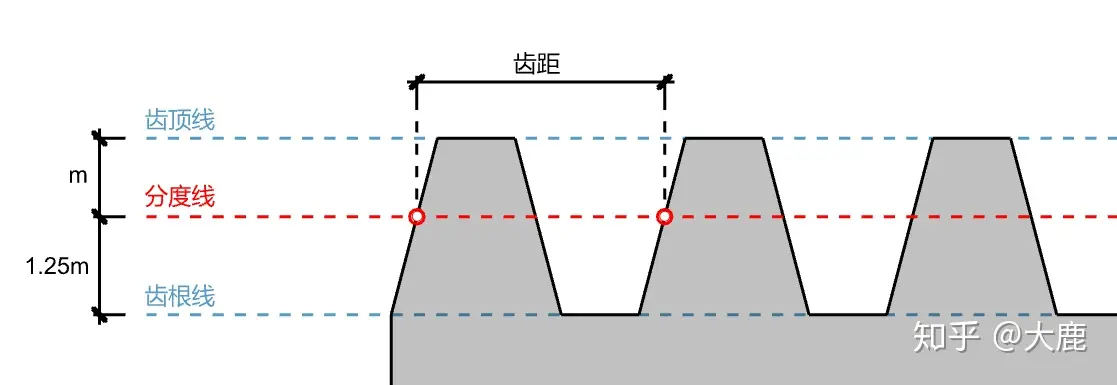
在决定齿条的垂直方向尺寸后,我们来看水平方向。
齿距可以从字面意思理解,为相邻两个齿的间距。我们利用之前已经掌握的分度线来做定位,分度线和齿一侧斜线的交点为上图红点,相邻两个红点的距离即为齿距。
标准齿轮的齿距计算公式和模数也有直接关系:
齿距=模数 x 圆周率
P=π×mP=\pi \times m
是不是发现到这里突然冷不丁冒出了圆周率。关于这一概念,我们会在下一章节齿轮的部分着重展开。在这里大家只需要明确齿距=模数x圆周率即可。
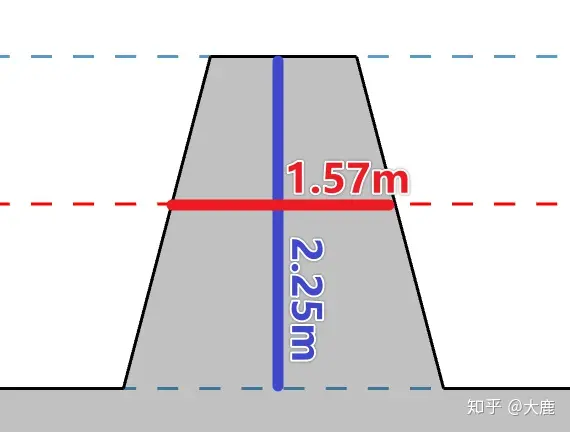
细心的观众会发现,其实按照这么来看,每个齿条上的齿比例是确定的。
梯形的高度=2.25m
4:5位置分度线所在位置的宽度=1.57m
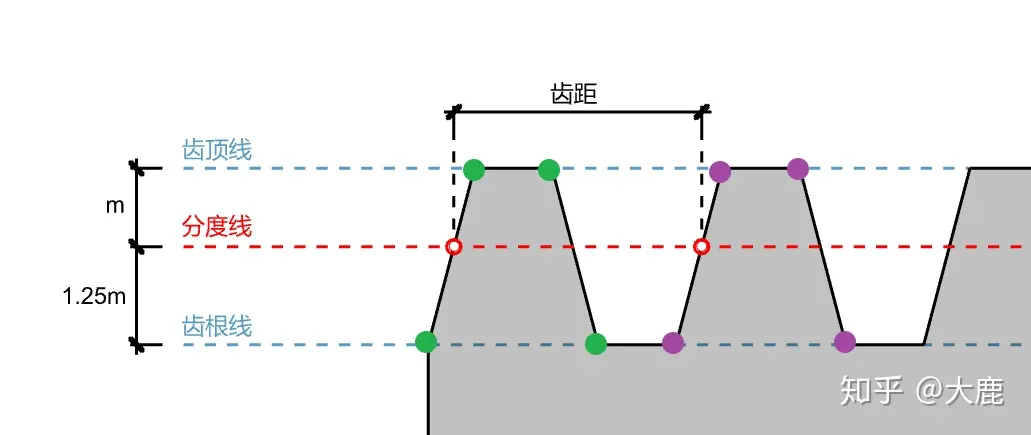
当然对齿条来说,我们用齿轮的另外四个角点做定位,例如上图绿色和紫色的距离,也能表达齿距。但这并不是一个好习惯,因为齿条很特殊是一条直线,所以齿顶距离,齿根距离等等都等于齿距,但对齿轮这样的圆形物体来说,齿顶和齿根的距离就完全和齿距是不同的概念。
因此哪怕是直线型的齿条,我们也应该以分度线作为齿距的计算标准,以保证后续概念拓展时不会出现差错。

如上图,齿厚比较简单,对标准的齿轮来说,齿厚=齿距 / 2

因为常年使用电脑的关系,我的肉眼已经在现实世界中严重削弱,很难分辨眼前的人是男是女。但在虚拟世界中我的眼睛就可以在瞬间分辨出,上图的齿厚不等于0.5倍齿距。

果然如此,眼看着作为教学的齿条竟然不符合科学道理。
看来就算是看似简单的齿条,也不能随手画。

这一个我随意绘制的齿条,采用的是我们最常见的名叫“想当然”的方法。
我做了一个不正确的假定,也就是蓝色的齿顶宽度=蓝色的齿根宽度。仔细看过上文会发现,没有一处有提到齿顶和齿根高度是相同的。在这个假定的基础上,只有绿色的中线作为分度线,才能确保齿厚=齿距的一半。
但实际上分度线并不是齿的中线,而是在4:5的位置,此时齿厚就不可能等于齿距的一半了。
6:实践
枯燥的理论终于看完了,进入了令人愉快的实践阶段。

首先绘制一张灵魂草图。我们的目标齿条有5个齿顶,4个齿根组成。
有很多GH玩家喜欢一上来就对着电脑,噼噼啪啪的开始操作。
我认为不妨关闭电子设备,电脑手机什么的,返璞归真,用铅笔和纸张画画草图,打打草稿。而不要像我这么懒直接在犀牛中绘制。

如上图,分度线和齿条之间有10个交点,分成了9段,自然就是5个齿顶和4个齿根。第一张草图画到这个程度就差不多OK了。
可能看到这已经忘了,此时我们应该先确定三大基本概念。齿数,模数和压力角。
对齿条来说,我们之前提到过,不应该使用齿数这个概念,因此齿数在这里跳过。


使用上文介绍的模数和压力角配置。
按照概念介绍的顺序,我们绘制一条分度线。根据草图,分度线被分成9等分,有10个点组成。而每个点的间距其实就是齿厚(不是齿距)。

在这里我们要注意,上文分析时的顺序是先介绍分度线,齿顶线和齿根线,后介绍齿距和齿厚,是为了方便概念的理解。但是在制作阶段,更加合理的方法是先使用齿距和齿厚确定分度线/齿轮轮廓线和分度线的交点,也就是上图的红色点。

先将齿距和齿厚计算出来。齿距=pi x 模数,齿厚=齿距/2

我们要将刚才灵魂草图上的参数关系明确到程序中,齿顶数量=5的情况下,会有9个交点,公式关系为2x+1。
在得到各项交点后,我们直接使用压力角生成齿轮的左右两条侧面曲线。

注意齿轮的左右是倾斜角度不同的,因此压力角简单做一个正负的处理即可。

理论研究看似复杂,但有助于我们清晰地理解问题,逻辑清晰后,程序的编写将会非常清爽整洁。

此时就可以把齿顶和齿根高计算出来。

在这里我们直接求齿顶和齿根平面,程序会更简洁。
注意GH内默认XZ平面的法向为-Y,而不是+Y。因此沿着Y正向的齿顶反而要给负数。

如上图,使用PLX直接求出交点,然后连线,注意数据结构处理(Graft)

如上图,不乏会有使用多年的职业选手选择一通狂连,企图猜对。

然而仔细分析问题,发现可以简单粗暴。拍平后发现只需要沿着X排序即可,偷懒的可以直接sort points,因为他的内部算法就是优先x方向排序。

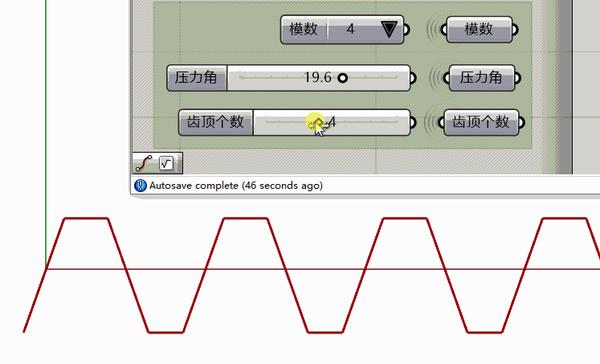
发现简简单单就这么完成了。除了齿的个数不太对。

实际上是个粗心错误,5个齿顶+4个齿根=9个分段=10个点。在这里不应该2x-1而是直接2x即可

至此这个5齿的齿条就生成完毕了。该齿条的模数=2,压力角=20。
我们尝试测量一下这个齿条的齿顶和齿根的宽度。

事实证明标准齿条的齿顶和齿根必然是不同的宽度,如果不采用上述方法绘制,将无法得到正确的尺寸。
下篇地址:
 722023-10-02 03:24:31
722023-10-02 03:24:31











